We illustrate how the specific values for a single object-oriented instance attribute are determined. We do this for the specific case of the “wLeft” instance attribute for the Node object in the 1-D cluster variation method (1D CVM) code. The same considerations will apply when we progress to the 2D CVM code.
The specific values for which we illustrate process here are for wLeft, which is one of several instance attributes for the Python object-oriented class Node.
This blogpost accompanies the YouTube “Code Walkthrough: 1-D Cluster Variation Method Object-Oriented Node Attributes.”
Constructing a 1-D Cluster Variation Method Grid
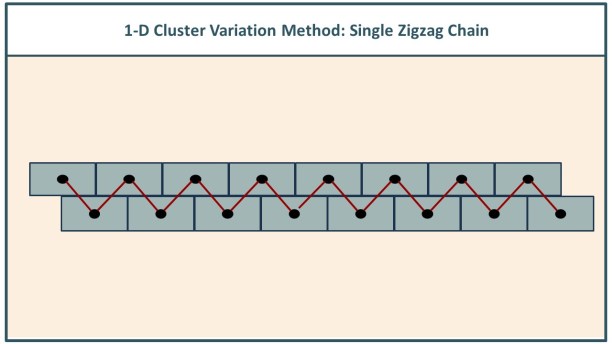
A cluster variation method (CVM) grid will be composed of layers of zigzag chains.
A 1D CVM grid, which we address as a starting point, is comprised of a single zigzag chain, as show in the following Figure 1.
CVM Configuration Variables
There are four different types of local configuration variables in the cluster variation method:
- xi – activation (“on” or “off”) of a given node (also referred to as a “unit”).
- yi – nearest-neighbor interactions,
- wi – next-nearest-neighbor interactions, and
- zi – triplet interactions.
Figure 2 shows each of these kinds of local configuration variables.

The yi (nearest-neighbor interactions) are actually between a node and nodes in the row above or below that node.
The wi (next-nearest neighbor interactions) are those between a node and its neighboring nodes in the same row. (When we get to 2D CVM grids, this will expand to include rows that are two rows above and two rows below a given node’s row.)
The zi (triplets) will involve multiple rows.
Object-Oriented Nodes in the CVM Code
We take an object-oriented approach, using Python, to creating Node objects in our CVM code.
In this blogpost, we walk through how we compute a single instance attribute – wLeft – for a given Node instance.

Determining wLeft Attribute Values
The YouTube referenced at the beginning of this blogpost provides a detailed walkthrough for computing the wLeft attribute for each node in a 1-D CVM grid.
Resources and References
Themesis GitHub Repository
AJM’s Note: This is new. This is the first time that we are pointing you to a code repository – with the intention that this will not just be code, but also PPTs (MS-PPTXTM) of how the code for computing local variables is based on the CVM (cluster variation method) grid architecture, code walkthroughs, worked examples, etc.
AJM’s Further Note: This code is the baseline for the interactive code, which is still (as of this writing) being added-on-to and debugged. HOWEVER, it’s got a fun little Python turtle graphics illustration of the 1-D CVM baseline that we’ll be using. The specific code is: simple-1D-CVM-w-Python-turtle-1pt3pt6-…
Prior Related YouTubes
Prior Related Blogposts
AJM’s Note: These blogposts were written ages ago – under AJM’s personal blogsite. We’ll be creating more materials soon.
- Maren, Alianna J. 2018. “Expressing Total Microstates (Omega) for the 1-D Cluster Variation Method – Part 1.” Alianna J. Maren Blogpost Series (Sept. 16, 2018). (Accessed Aug. 2, 2023; available online at https://www.aliannajmaren.com/2018/09/16/expressing-total-microstates-omega-1-d-cvm-part-1/.)
- Maren, Alianna J. 2018. “An Interesting Little Thing about the CVM Entropy (With Code).” Alianna J. Maren Blogpost Series (October 28, 2018). (Accessed Aug. 2, 2023; available online at https://www.aliannajmaren.com/2018/10/28/an-interesting-little-thing-about-the-cvm-entropy/ .)
AJM’s Note: Prior Themesis blogpost – a placeholder post – which will be moved (in date) to be NEXT WEEK’S POST as soon as we update the code and update the post.
- Maren, Alianna J. 2023. “1-D Cluster Variation Method (1D CVM): Code Soon!.” Themesis, Inc. Blogpost Series (Aug. 2, 2023). (Accessed Aug. 6, 2023; available online at https://themesis.com/2023/08/02/1-d-cluster-variation-method-1d-cvm-interactive-code/)
The Single Most Useful Research Paper
1-D Cluster Variation Method: Computational Result
- Maren, Alianna J. 2016. “The Cluster Variation Method: A Primer for Neuroscientists.” Brain Sci. 6(4), 44, https://doi.org/10.3390/brainsci6040044; online access, pdf; accessed 2018/09/19.
Two Important CVM Origination Papers
- Kikuchi, R. (1951). “A Theory of Cooperative Phenomena.” Phys. Rev. 81, 988-1003, pdf, accessed 2018/09/17.
- Kikuchi, Ryiochi., & Brush, Stephen G. 1967. “Improvement of the Cluster‐Variation Method,” J. Chem. Phys. 47(1), 195; online as: online – for purchase through American Inst. Physics. Costs $30.00 for non-members.
Challenge Exercise
For those who wish to gain more depth with a 1-D CVM grid, we suggest the following from Maren (2016):
- Scan the Intro, largely skipping the Brain-Computer Interface (BCI) paragraphs. (We believe that CORTECONs will be useful for BCI down the road, but that is not pertinent right now.)
- Lightly read Sect. 2.3. Neural Motifs, Topographies, and Pattern-Formation – this is general background, again not essential.
- Sect. 3, Statistical Mechanics for Neural Ensembles, is optional.
- READ Sect. 4, “Configuration Variables: Describing Local Patterns.”
- READ Sect. 5, “The Cluster Variation Method for a 1-D Zigzag Chain.”
- We’ll pick up with the analytic solutions and phase space discussions in later blogposts and YouTubes.
Thank you for joining! – AJM
The Most Powerful Reason for Doing This …
Let’s get serious.
There’s only one reason for working through this code, these equations: